Arbeitszeit: Zwei Schulstunden plus Hausaufgabenzeit
1) Bearbeite sorgfältig die untenstehende Aufgabe und beantworte
die Fragen im Heft:
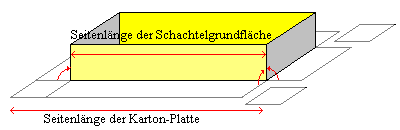
In einer Kartonfabrik werden aus quadratischen Karton-Platten durch
Herausschneiden von Quadraten an den Ecken und Hochklappen der Seitenteile
offene Schachteln mit quadratischer Grundfäche hergestellt.
Wie groß ist die Grundseite der Schachtel, wenn wir an den Ecken
1-dm-Quadrate herausschneiden und die Seite der Kartonplatte a) 1 m, b)
8 dm, c) 6 dm, d) x dm lang war?
Wie groß ist die Grundfläche der Schachtel bei a), b), c)
und d)?
(Vergleiche, nachdem du die Aufgabe gelöst hast,
mit deinem Nachbarn.) |
 |
2) Wir untersuchen die Schaubilder
Eine der Funktionen mit den Gleichungen a) y = (x - 1)2
, b) y = (x - 2)2 und c) y = (x - 3)2 beschreibt
die Herstellung der Schachteln oben.
a) Welche der Funktionen ist es? (Antwort ins Heft)
b) Fertige für die drei Funktionen Wertetabellen (für
x) von -3 bis 6.
c) Zeichne die Schaubilder der 3 Funktionen (in einer vernünftigen
Größe!!) in ein Koordinatensystem zusammen mit dem Schaubild
für y = x2 (insgesamt 4 Kurven)
d) Schreibe auf, welchen Scheitel die Parabeln jeweils haben.
e) Deine Parabel c) findest du als rote Kurve in der Abbildung
129.1 auf Seite 129 in deinem Buch (Diesterweg 9).
f) Wie kommte man von der Normalparabel y = x2
zu den Schaubildern der Funktionen a), b) und c)? (Antwort ins Heft)
g) Zeichne mit der Parabelschablone das Schaubild der Funktion
mit der Gleichung y = (x - 5)2 in das Koordinatensystem.
(Vergleiche, nachdem du die Aufgabe gelöst hast,
mit deinem Nachbarn.)
3) a) Versuche den folgenden Merksatz zu verstehen
Die Funktion x 
(x - x0)2 mit der Gleichung y = (x - x0)2
nimmt ihren kleinsten Funktionswert 0
für x = x0 an. Ihr Schaubild ist
eine Normalparabel mit dem Scheitel S ( x0 ; 0). |
b) Zeichne nach diesem Merksatz das Schaubild zur Funktion
y = (x - (- 3))2 mit Hilfe der Parabelschablone.
c) Begründe schriftlich, warum die Funktionen y =
(x - (- 3))2 und y = (x + 3)2 gleich sind.
d) Wende den Merksatz oben auf die Funktion y = (x - (-
2))2 an.
e) Zeichne mit der Parabelschablone die Schaubilder zu
y = (x + 1)2 und y = (x +2,5)2 .
(Vergleiche, nachdem du die Aufgabe gelöst hast,
mit deinem Nachbarn.)
4a) Begründe, warum die Funktionen y = (x - 3)2
und y = x2 - 6x + 9 nur verschiedene Schreibweisen
für die gleiche Funktion sind.
b) Wandle die Funktionsgleichung y = x2
- 4x + 4 so um, dass sie das Merksatzschema oben erfüllt und
bestimme den Scheitel und gib an in welche Richtung sie verschoben wurde.
c) Verfahre ebenso für y = x2 -
10x + 25 , y = x2 + 8x + 16 und
y = x2 - 3x + 2,25.
(Vergleiche, nachdem du die Aufgabe gelöst hast,
mit deinem Nachbarn.)
[Haftungsausschluss] [Datenschutz]